Celebrating a Century
of Quantum Discoveries
of Quantum Discoveries
Advancing Quantum Research Through Open Access Publishing.

The formal development of quantum mechanics began in 1925 with Werner Heisenberg’s matrix formulation, laying the foundation for a revolutionary understanding of the physical world. Over the past century, quantum theory has become central to modern physics, driving advances in quantum computing, cryptography, and materials science.
As quantum research continues to grow in complexity and significance, open access publishing plays a critical role in accelerating scientific progress. At MDPI, we are committed to ensuring the latest advances in quantum mechanics are freely accessible to the global research community—fostering collaboration, transparency, and innovation across disciplines.
Take a scroll down memory lane with us to discover the marvels of quantum physics since before 1925.
News & Events
Special Issues
Topics
Research Highlight
A Review of the Current State of Magnetic Force Microscopy to Unravel the Magnetic Properties of Nanomaterials Applied in Biological Systems and Future Directions for Quantum Technologies
Abstract: Magnetism plays a pivotal role in many biological systems. However, the intensity of the magnetic forces exerted between magnetic bodies is usually low, which demands the development of ultra-sensitivity tools for proper sensing. In this framework, magnetic force microscopy (MFM) offers excellent lateral resolution and the possibility of conducting single-molecule studies like other single-probe microscopy (SPM) techniques. This comprehensive review attempts to describe the paramount importance of magnetic forces for biological applications by highlighting MFM’s main advantages but also intrinsic limitations. While the working principles are described in depth, the article also focuses on novel micro- and nanofabrication procedures for MFM tips, which enhance the magnetic response signal of tested biomaterials compared to commercial nanoprobes. This work also depicts some relevant examples where MFM can quantitatively assess the magnetic performance of nanomaterials involved in biological systems, including magnetotactic bacteria, cryptochrome flavoproteins, and magnetic nanoparticles that can interact with animal tissues. Additionally, the most promising perspectives in this field are highlighted to make the reader aware of upcoming challenges when aiming toward quantum technologies.
Nanomaterials
Published on 18 September 2023
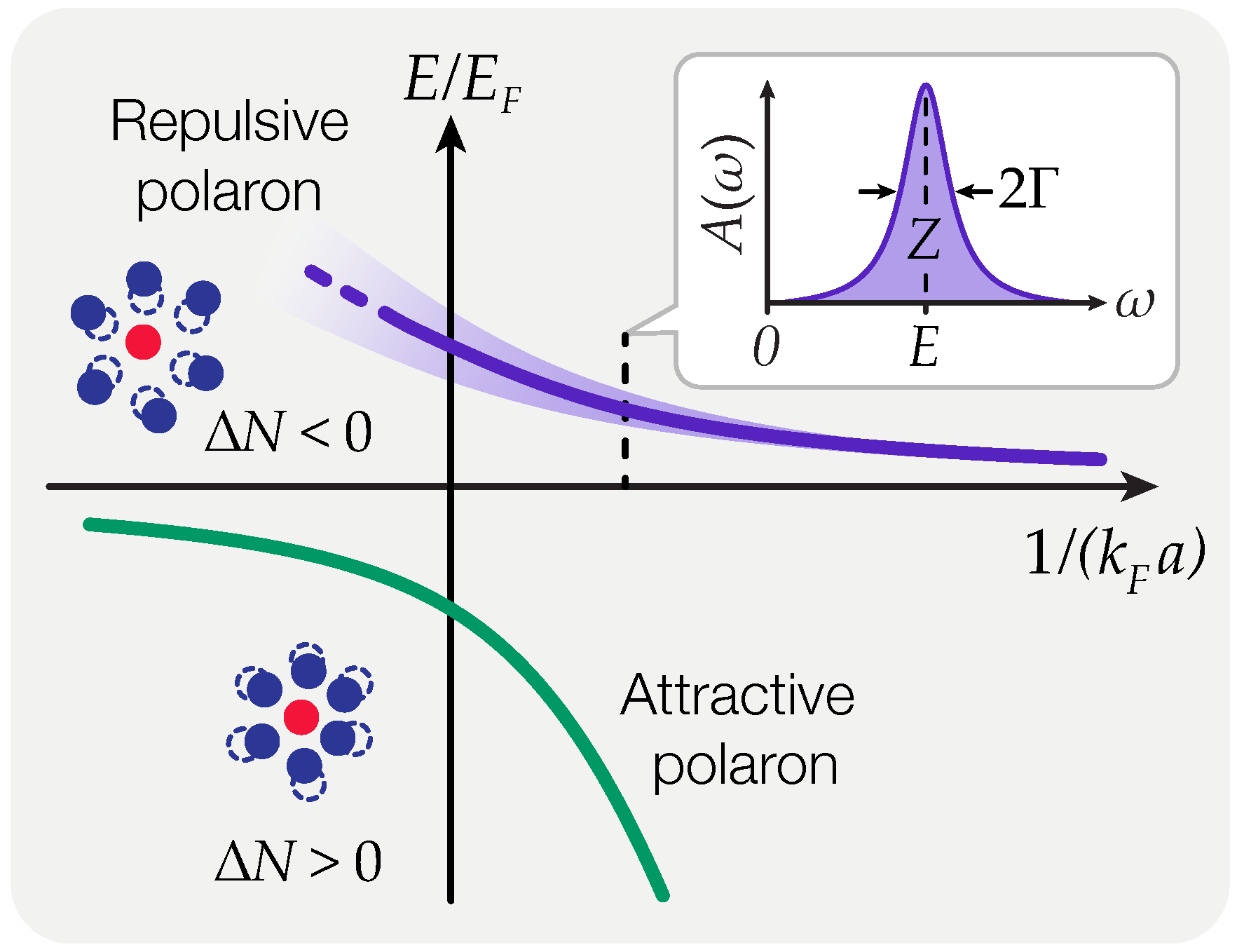
Repulsive Fermi and Bose Polarons in Quantum Gases
Abstract: Polaron quasiparticles are formed when a mobile impurity is coupled to the elementary excitations of a many-particle background. In the field of ultracold atoms, the study of the associated impurity problem has attracted a growing interest over the last fifteen years. Polaron quasiparticle properties are essential to our understanding of a variety of paradigmatic quantum many-body systems realized in ultracold atomic gases and in the solid state, from imbalanced Bose–Fermi and Fermi–Fermi mixtures to fermionic Hubbard models. In this topical review, we focus on the so-called repulsive polaron branch, which emerges as an excited many-body state in systems with underlying attractive interactions such as ultracold atomic mixtures, and is characterized by an effective repulsion between the impurity and the surrounding medium. We give a brief account of the current theoretical and experimental understanding of repulsive polaron properties, for impurities embedded in both fermionic and bosonic media, and we highlight open issues deserving future investigations.
Atoms
Published on 27 May 2022
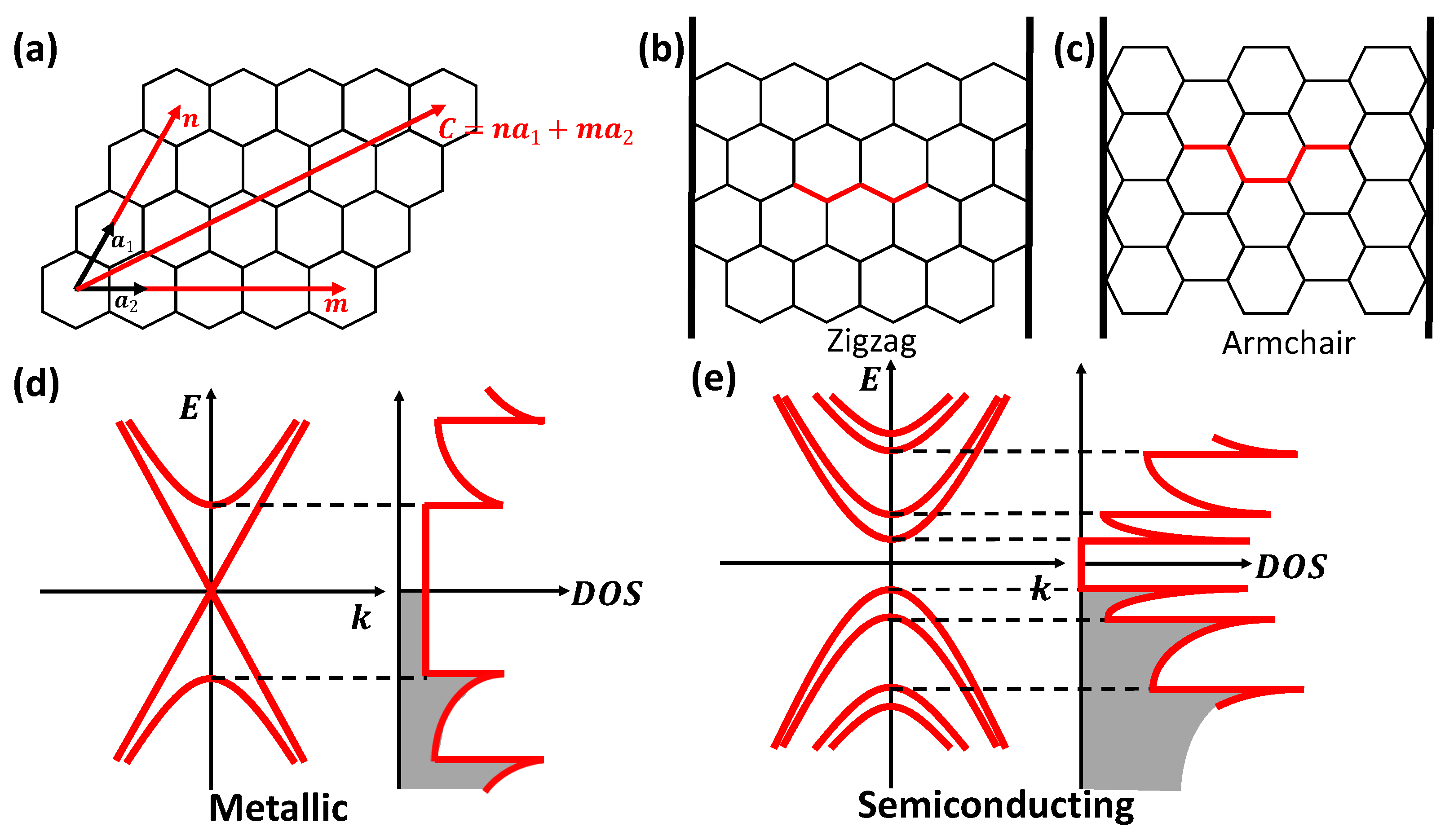
Carbon Nanotube Devices for Quantum Technology
Abstract: Carbon nanotubes, quintessentially one-dimensional quantum objects, possess a variety of electrical, optical, and mechanical properties that are suited for developing devices that operate on quantum mechanical principles. The states of one-dimensional electrons, excitons, and phonons in carbon nanotubes with exceptionally large quantization energies are promising for high-operating-temperature quantum devices. Here, we discuss recent progress in the development of carbon-nanotube-based devices for quantum technology, i.e., quantum mechanical strategies for revolutionizing computation, sensing, and communication. We cover fundamental properties of carbon nanotubes, their growth and purification methods, and methodologies for assembling them into architectures of ordered nanotubes that manifest macroscopic quantum properties. Most importantly, recent developments and proposals for quantum information processing devices based on individual and assembled nanotubes are reviewed.
Materials
Published on 18 February 2022
Time in Quantum Cosmology
Abstract: Time in quantum gravity is not a well-defined notion despite its central role in the very definition of dynamics. Using the formalism of quantum geometrodynamics, we briefly review the problem and illustrate it with two proposed solutions. Our main application is quantum cosmology—the application of quantum gravity to the Universe as a whole.
Universe
Published on 08 January 2022
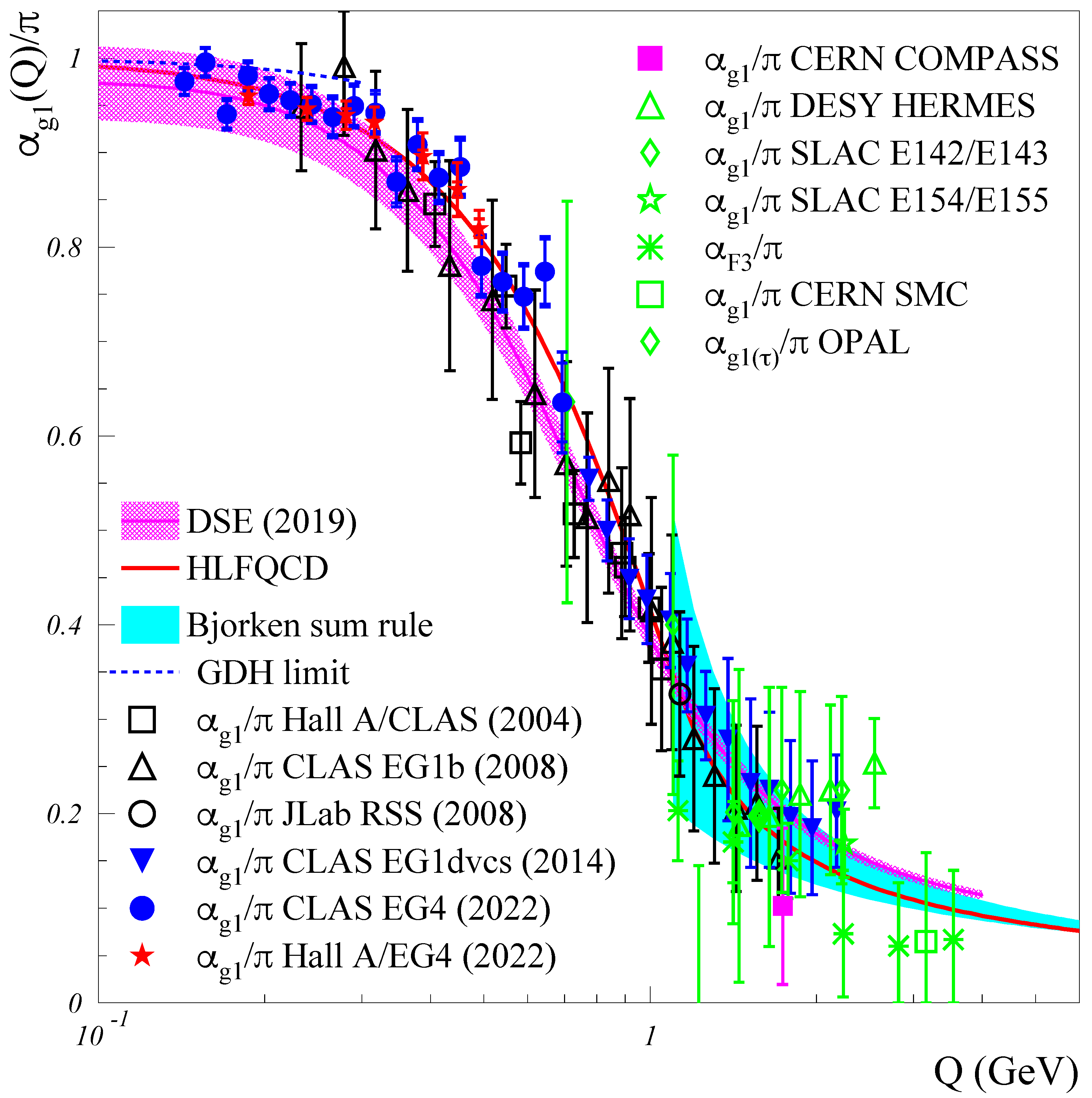
Experimental Determination of the QCD Effective Charge αg1(Q)
Abstract: The QCD effective charge
Particles
Published on 31 May 2022
Contextuality, Complementarity, Signaling, and Bell Tests
Abstract: This is a review devoted to the complementarity–contextuality interplay with connection to the Bell inequalities. Starting the discussion with complementarity, I point to contextuality as its seed. Bohr contextuality is the dependence of an observable’s outcome on the experimental context; on the system–apparatus interaction. Probabilistically, complementarity means that the joint probability distribution (JPD) does not exist. Instead of the JPD, one has to operate with contextual probabilities. The Bell inequalities are interpreted as the statistical tests of contextuality, and hence, incompatibility. For context-dependent probabilities, these inequalities may be violated. I stress that contextuality tested by the Bell inequalities is the so-called joint measurement contextuality (JMC), the special case of Bohr’s contextuality. Then, I examine the role of signaling (marginal inconsistency). In QM, signaling can be considered as an experimental artifact. However, often, experimental data have signaling patterns. I discuss possible sources of signaling—for example, dependence of the state preparation on measurement settings. In principle, one can extract the measure of “pure contextuality” from data shadowed by signaling. This theory is known as contextuality by default (CbD). It leads to inequalities with an additional term quantifying signaling: Bell–Dzhafarov–Kujala inequalities.
Entropy
Published on 28 September 2022
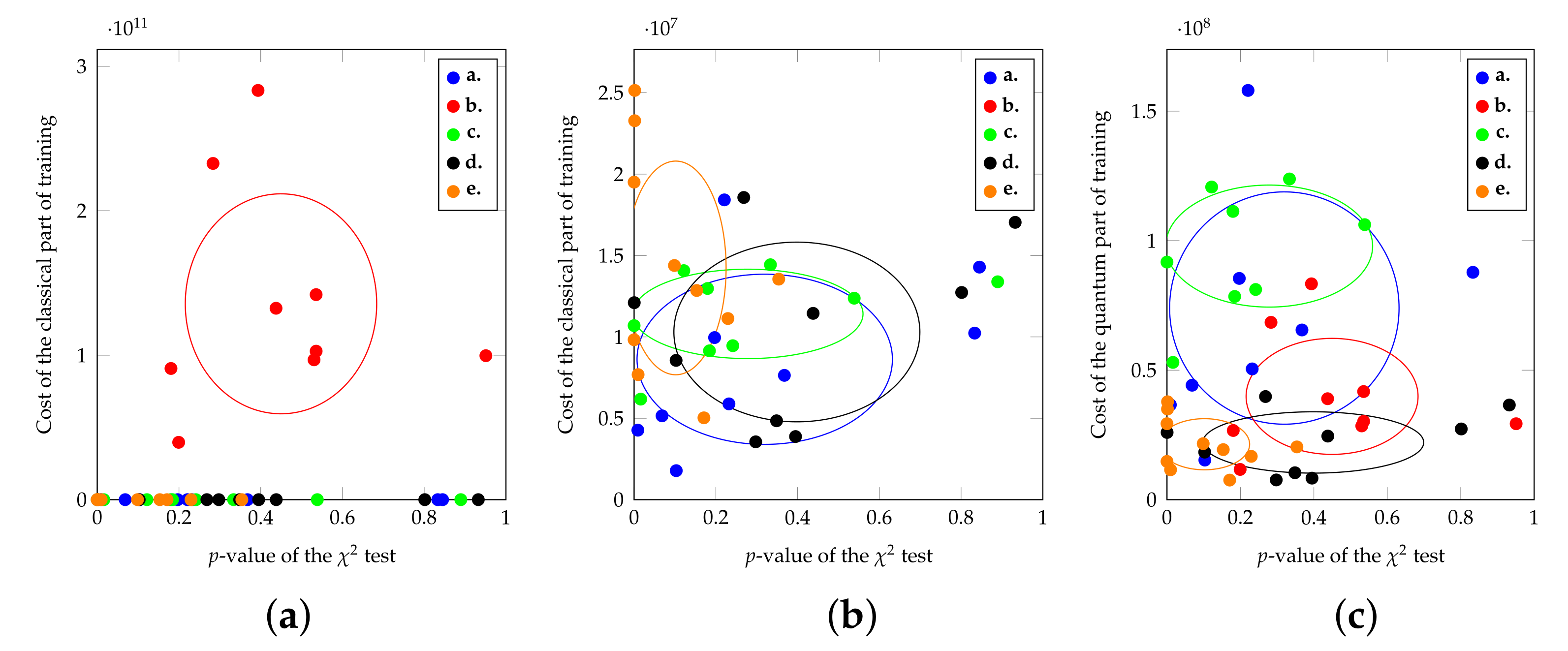
Optimal Tuning of Quantum Generative Adversarial Networks for Multivariate Distribution Loading
Abstract: Loading data efficiently from classical memories to quantum computers is a key challenge of noisy intermediate-scale quantum computers. Such a problem can be addressed through quantum generative adversarial networks (qGANs), which are noise tolerant and agnostic with respect to data. Tuning a qGAN to balance accuracy and training time is a hard task that becomes paramount when target distributions are multivariate. Thanks to our tuning of the hyper-parameters and of the optimizer, the training of qGAN reduces, on average, the Kolmogorov–Smirnov statistic of 43–64% with respect to the state of the art. The ability to reach optima is non-trivially affected by the starting point of the search algorithm. A gap arises between the optimal and sub-optimal training accuracy. We also point out that the simultaneous perturbation stochastic approximation (SPSA) optimizer does not achieve the same accuracy as the Adam optimizer in our conditions, thus calling for new advancements to support the scaling capability of qGANs.
Quantum Reports
Published on 09 February 2022
Introducing Quantum Technologies at Secondary School Level: Challenges and Potential Impact of an Online Extracurricular Course
Abstract: Stimulated by the European project “QTEdu CSA”, within the flagship “Quantum Technologies”, a community of researchers active in the fields of quantum technologies and physics education has designed and implemented an extracurricular course on quantum physics concepts and quantum technologies applications for high school. The course, which featured eight interactive lectures, was organized online between March and May 2021 and attended by about 250 students from all over Italy. In this paper, we describe the main tenets and activities of the course. Moreover, we report on the effectiveness of the course on students’ knowledge of the basic concepts of quantum physics and students’ views about epistemic aspects and applications of quantum technologies. Results show that the designed activities were effective in improving students’ knowledge about fundamental aspects of quantum mechanics and familiarizing them with quantum technology applications.
Physics
Published on 29 September 2022
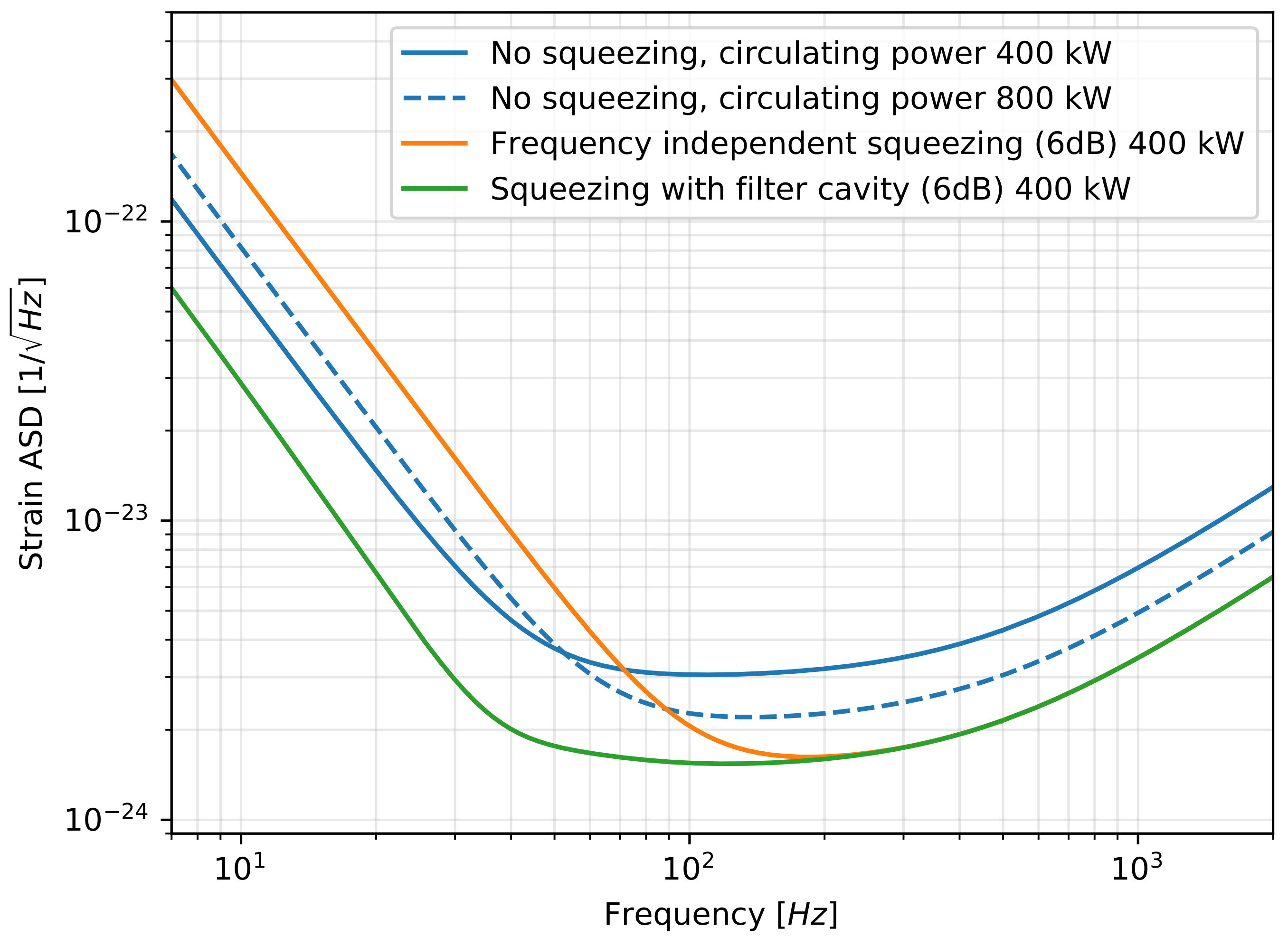
Squeezing in Gravitational Wave Detectors
Abstract: Injecting optical squeezed states of light, a technique known as squeezing, is now a tool for gravitational wave detection. Its ability to reduce quantum noise is helping to reveal more gravitational wave transients, expanding the catalog of observations in the last observing run. This review introduces squeezing and its history in the context of gravitational-wave detectors. It overviews the benefits, limitations and methods of incorporating squeezing into advanced interferometers, emphasizing the most relevant details for astrophysics instrumentation.
Galaxies
Published on 09 March 2022
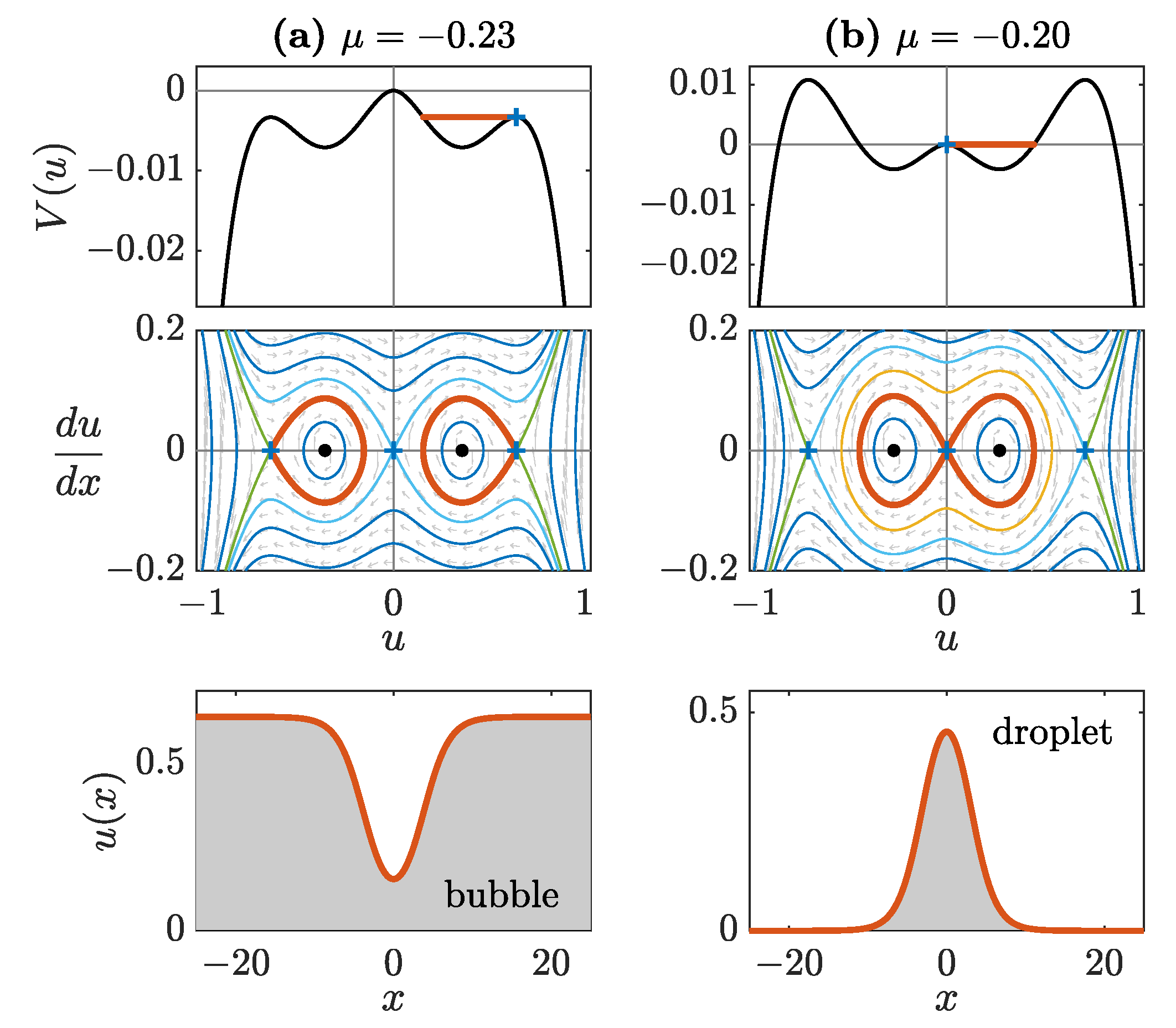
Interactions and Dynamics of One-Dimensional Droplets, Bubbles and Kinks
Abstract: We explore the dynamics and interactions of multiple bright droplets and bubbles, as well as the interactions of kinks with droplets and with antikinks, in the extended one-dimensional Gross–Pitaevskii model including the Lee–Huang–Yang correction. Existence regions are identified for the one-dimensional droplets and bubbles in terms of their chemical potential, verifying the stability of the droplets and exposing the instability of the bubbles. The limiting case of the droplet family is a stable kink. The interactions between droplets demonstrate in-phase (out-of-phase) attraction (repulsion), with the so-called Manton’s method explicating the observed dynamical response, and mixed behavior for intermediate values of the phase shift. Droplets bearing different chemical potentials experience mass-exchange phenomena. Individual bubbles exhibit core expansion and mutual attraction prior to their destabilization. Droplets interacting with kinks are absorbed by them, a process accompanied by the emission of dispersive shock waves and gray solitons. Kink–antikink interactions are repulsive, generating counter-propagating shock waves. Our findings reveal dynamical features of droplets and kinks that can be detected in current experiments.
Condensed Matter
Published on 04 August 2023
High Power Mid-Infrared Quantum Cascade Lasers Grown on GaAs
Abstract: The motivation behind this work is to show that InP-based intersubband lasers with high power can be realized on substrates with significant lattice mismatch. This is a primary concern for the integration of mid-infrared active optoelectronic devices on low-cost photonic platforms, such as Si. As evidence, an InP-based mid-infrared quantum cascade laser structure was grown on a GaAs substrate, which has a large (4%) lattice mismatch with respect to InP. Prior to laser core growth, a metamorphic buffer layer of InP was grown directly on a GaAs substrate to adjust the lattice constant. Wafer characterization data are given to establish general material characteristics. A simple fabrication procedure leads to lasers with high peak power (>14 W) at room temperature. These results are extremely promising for direct quantum cascade laser growth on Si substrates.
Photonics
Published on 01 April 2022

Selected Concepts of Quantum State Tomography
Abstract: Quantum state tomography (QST) refers to any method that allows one to reconstruct the accurate representation of a quantum system based on data obtainable from an experiment. In this paper, we concentrate on theoretical methods of quantum tomography, but some significant experimental results are also presented. Due to a considerable body of literature and intensive ongoing research activity in the field of QST, this overview is restricted to presenting selected ideas, methods, and results. First, we discuss tomography of pure states by distinguishing two aspects—complex vector reconstruction and wavefunction measurement. Then, we move on to the Wigner function reconstruction. Finally, the core section of the article is devoted to the stroboscopic tomography, which provides the optimal criteria for state recovery by including the dynamics in the scheme. Throughout the paper, we pay particular attention to photonic tomography, since multiple protocols in quantum optics require well-defined states of light.
Optics
Published on 25 August 2022
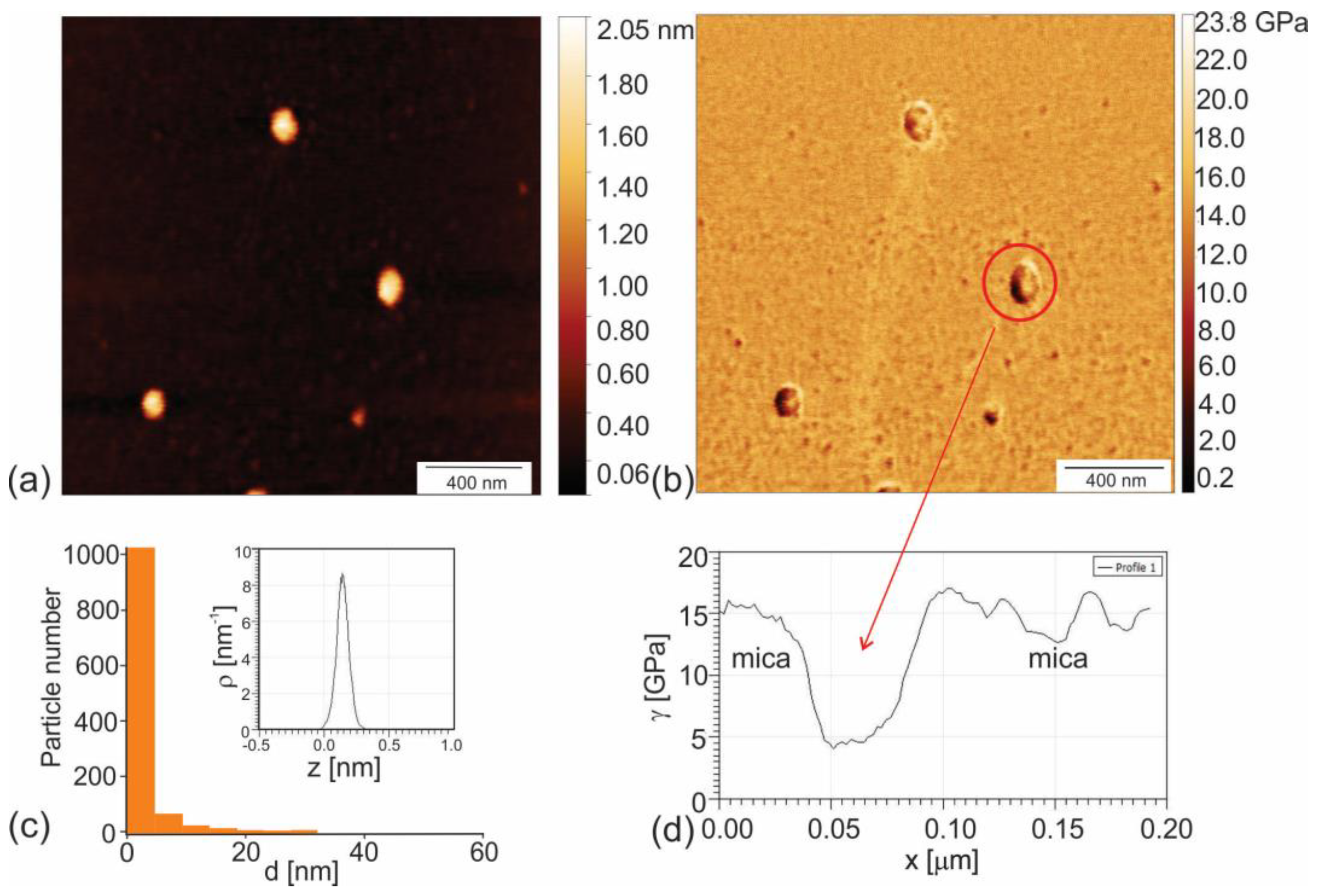
Phloroglucinol-Based Carbon Quantum Dots/Polyurethane Composite Films: How Structure of Carbon Quantum Dots Affects Antibacterial and Antibiofouling Efficiency of Composite Films
Abstract: Nowadays, bacteria resistance to many antibiotics is a huge problem, especially in clinics and other parts of the healthcare system. This critical health issue requires a dynamic approach to produce new types of antibacterial coatings to combat various pathogen microbes. In this research, we prepared a new type of carbon quantum dots based on phloroglucinol using the bottom-up method. Polyurethane composite films were produced using the swell–encapsulation–shrink method. Detailed electrostatic force and viscoelastic microscopy of carbon quantum dots revealed inhomogeneous structure characterized by electron-rich/soft and electron-poor/hard regions. The uncommon photoluminescence spectrum of carbon quantum dots core had a multipeak structure. Several tests confirmed that carbon quantum dots and composite films produced singlet oxygen. Antibacterial and antibiofouling efficiency of composite films was tested on eight bacteria strains and three bacteria biofilms.
Polymers
Published on 11 June 2024
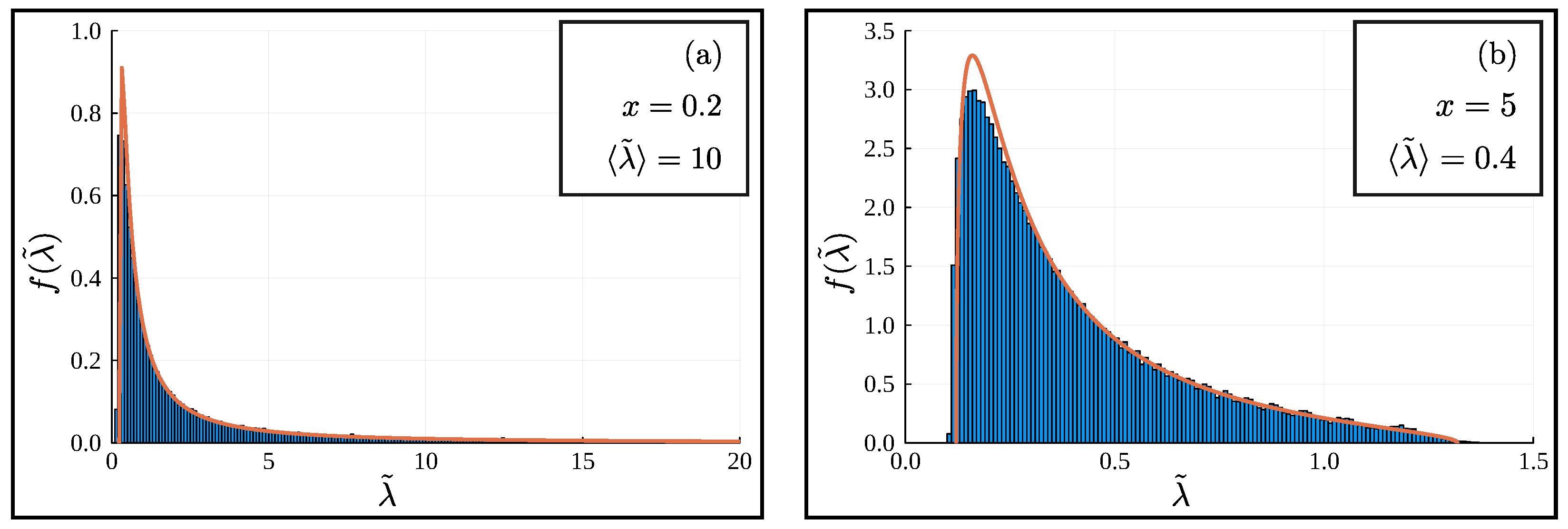
A Dyson Brownian Motion Model for Weak Measurements in Chaotic Quantum Systems
Abstract: We consider a toy model for the study of monitored dynamics in many-body quantum systems. We study the stochastic Schrödinger equation resulting from continuous monitoring with a rate
Quantum Reports
Published on 16 May 2024
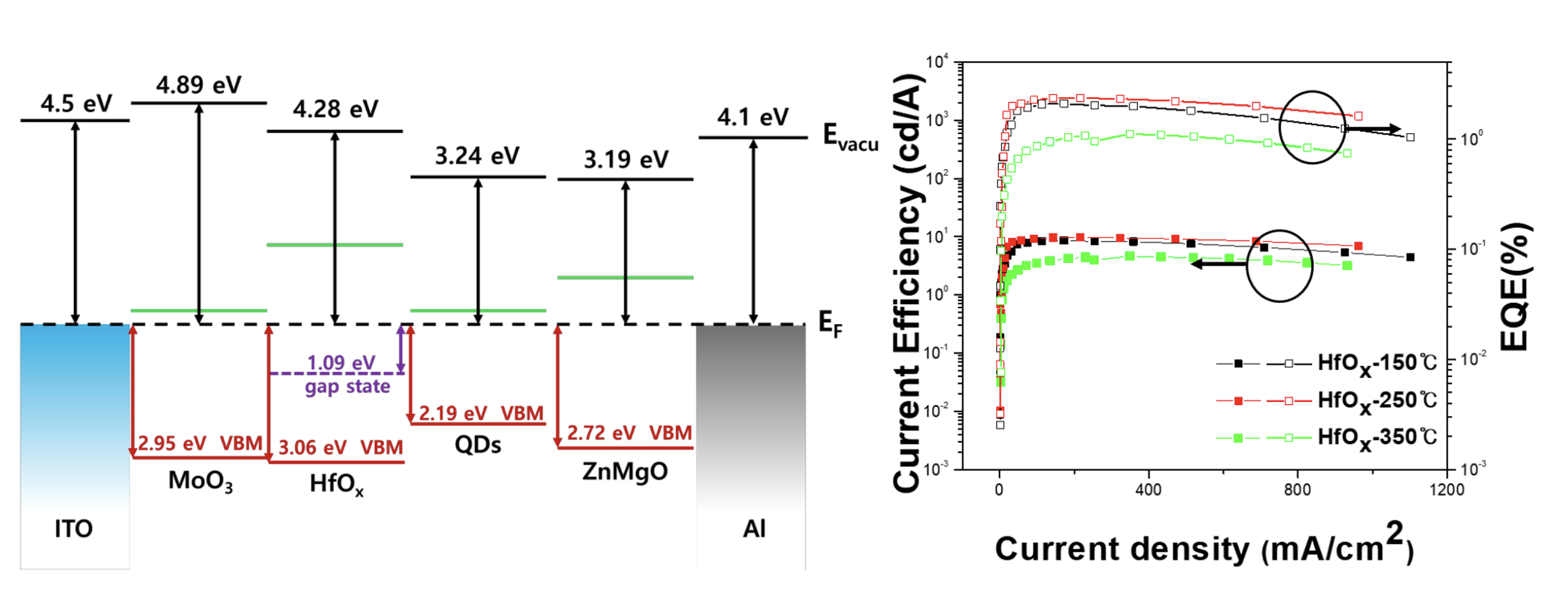
Improvement of the Stability of Quantum-Dot Light Emitting Diodes Using Inorganic HfOx Hole Transport Layer
Abstract: One of the major challenges in QLED research is improving the stability of the devices. In this study, we fabricated all inorganic quantum-dot light emitting diodes (QLEDs) using hafnium oxide (HfOx) as the hole transport layer (HTL), a material commonly used for insulator. Oxygen vacancies in HfOx create defect states below the Fermi level, providing a pathway for hole injection. The concentration of these oxygen vacancies can be controlled by the annealing temperature. We optimized the all-inorganic QLEDs with HfOx as the HTL by changing the annealing temperature. The optimized QLEDs with HfOx as the HTL showed a maximum luminance and current efficiency of 66,258 cd/m2 and 9.7 cd/A, respectively. The fabricated all-inorganic QLEDs exhibited remarkable stability, particularly when compared to devices using organic materials for the HTL. Under extended storage in ambient conditions, the all-inorganic device demonstrated a significantly enhanced operating lifetime (T50) of 5.5 h, which is 11 times longer than that of QLEDs using an organic HTL. These results indicate that the all-inorganic QLEDs structure, with ITO/MoO3/HfOx/QDs/ZnMgO/Al, exhibits superior stability compared to organic-inorganic hybrid QLEDs.
Materials
Published on 27 September 2024
History of Quantum Mechanics

(1900) The Ultraviolet Catastrophe and Planck’s Solution
Max Planck proposed the quantum hypothesis to explain the blackbody radiation problem and introduced the concept of "energy quantization" for the first time.
This revolutionary idea laid the foundation for quantum mechanics, introducing the concept that energy levels in nature are quantized rather than continuous.

(1905) Einstein’s Photoelectric Effect and Wave-Particle Duality
Albert Einstein extended Planck’s ideas. He proposed the light quantum hypothesis (photon) to explain the photoelectric effect and further support the quantum concept.
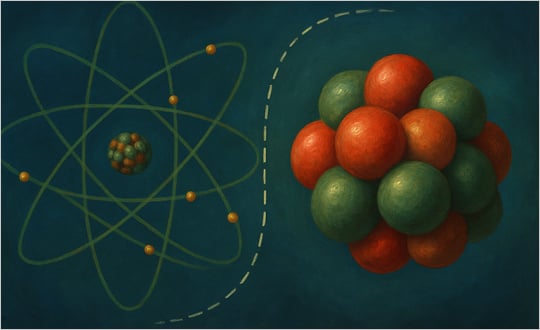
(1913) Bohr’s Quantum Model of the Atom
Niels Bohr proposed the Bohr model of the atomic structure, introducing quantization conditions into atomic orbitals and explaining the spectrum of hydrogen atoms, also reinforcing the necessity of quantization in atomic physics.

(1925 - 1926) The Birth of Quantum Mechanics: Heisenberg and Schrödinger
Werner Heisenberg formulated matrix mechanics (quantum mechanics in matrix form), marking the birth of the mathematical framework of quantum mechanics. Erwin Schrödinger developed wave mechanics (Schrödinger equation), using wave functions to describe quantum states, which was later proved to be equivalent to matrix mechanics.
This new framework replaced classical determinism with a probabilistic view of nature, fundamentally altering our understanding of atomic and subatomic behavior and paving the way for modern quantum physics.

(1927) A Significant Turning Point in the Understanding of Quantum Mechanics
Heisenberg proposed the uncertainty principle, which showed that it is impossible to accurately measure the position and momentum of a particle at the same time and became a cornerstone of the Copenhagen interpretation of quantum mechanics.
Bohr proposed the complementarity principle at the Solvay Conference, which led to the Copenhagen interpretation (the standard interpretation of quantum mechanics).
This year marked a significant turning point in the understanding of quantum mechanics, leading to profound insights into the nature of reality at the atomic and subatomic levels.
(1928) Dirac’s Relativistic Quantum Mechanics and Antimatter Prediction
Paul Dirac combined quantum mechanics and relativity to propose relativistic quantum mechanics (Dirac equation).
The Dirac equation elegantly combined quantum mechanics with special relativity, resolving inconsistencies between the two theories and introducing the concept of negative energy states.

(1935) The EPR Paradox and Quantum Entanglement
Albert Einstein, Boris Podolsky, and Nathan Rosen published a paper challenging the completeness of quantum mechanics, introducing what became known as the EPR paradox. They argued that certain pairs of physical properties, such as position and momentum, could not be precisely measured simultaneously, leading them to believe that quantum theory was incomplete. The EPR paradox remains a cornerstone of quantum physics, challenging our understanding of reality and sparking ongoing research into the nature of quantum entanglement and its potential applications.
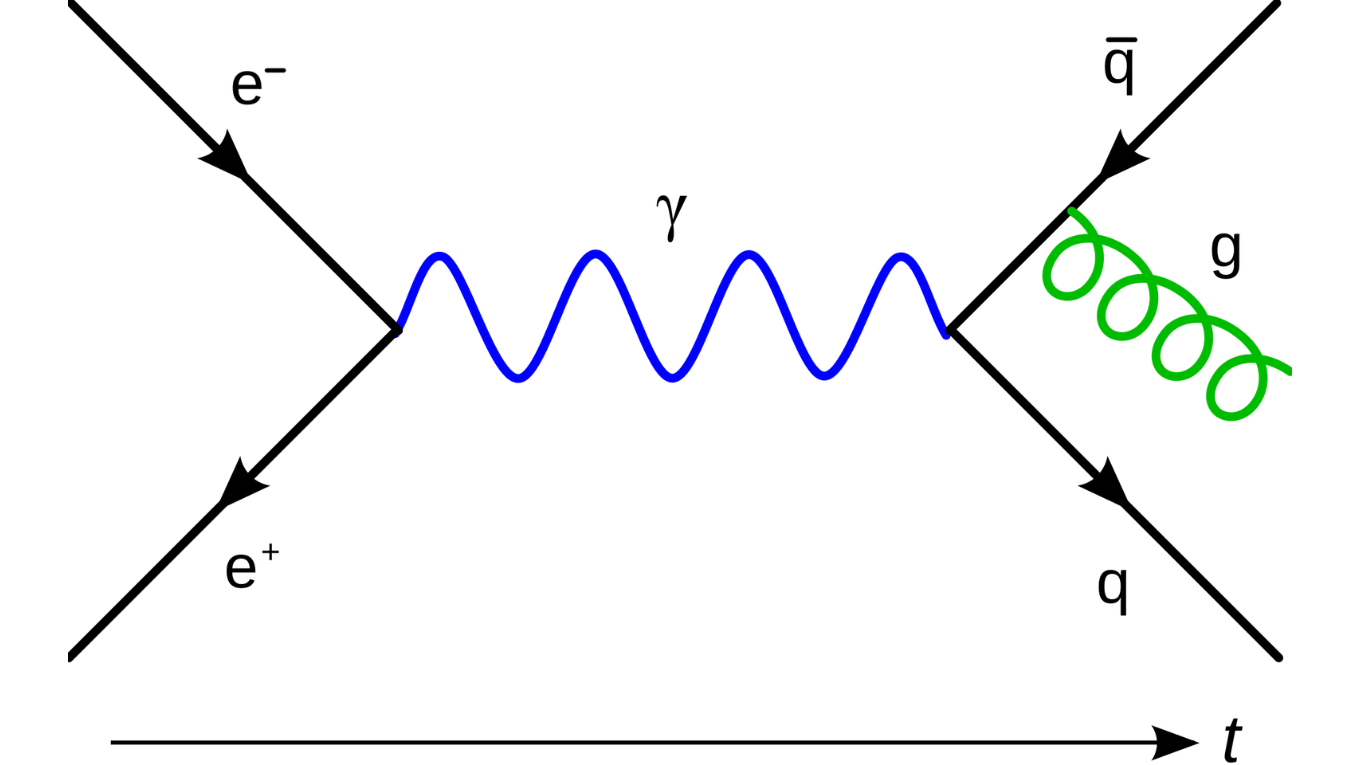
(1940s - 1950) Quantum Electrodynamics (QED) and Renormalization
Richard Feynman, Julian Schwinger, and Sin-Itiro Tomonaga developed quantum electrodynamics (QED), a quantum field theory describing how light and matter interact, to solve the problem of electromagnetic interaction.
QED became the first quantum field theory to achieve precise agreement with experimental results, setting the stage for the development of the Standard Model of particle physics.

(1981 - Present) Quantum Computing and the Future
In 1981, Richard Feynman proposed a model for a "quantum computer" to simulate quantum systems and proposed the concept of quantum computing.
This idea kicked off the work to develop quantum algorithms, and marks the ongoing evolution of quantum technologies.

(2025) Celebrating a Century of Quantum Discoveries
Today, quantum science and technology are rapidly evolving, moving from research labs to industrial applications such as cryptography, optimization, and materials science. In 2025, the world marks the centennial of quantum mechanics.
Aligned with the International Year of Quantum Science & Technology (IYQ), MDPI proudly commemorates this occasion by highlighting our dedication to open access publishing and the dissemination of quantum research.






































